Atom interferometry in 1D harmonic trap

---

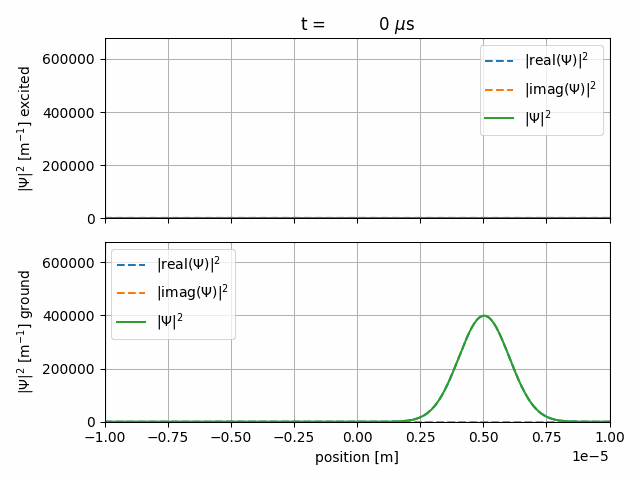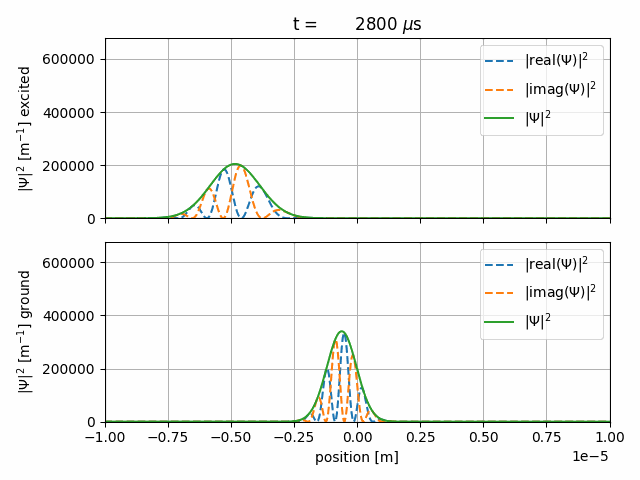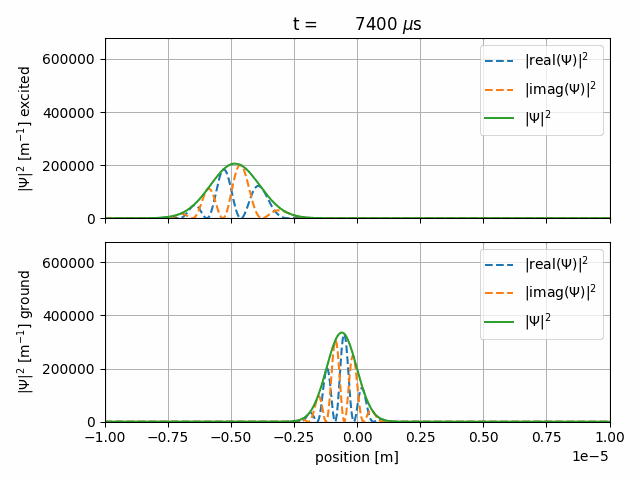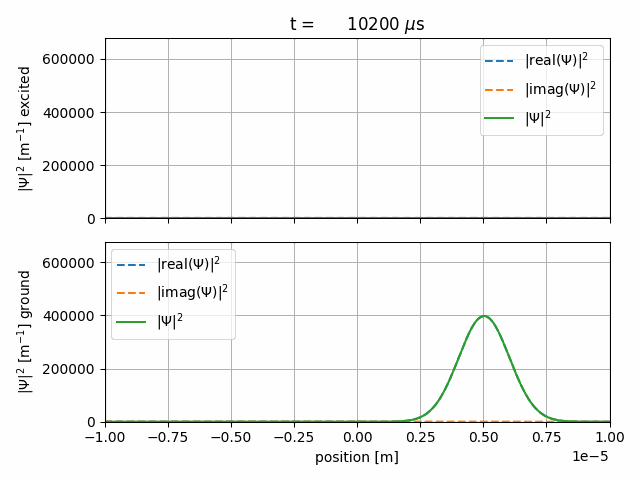
(You can find corresponding files in the TALISES examples folder)
In this example we put a Gaussian wave-packet into a superposition of two internal states and switch on an harmonic potential. As a twist we make the excited state twice as susceptible to the harmonic potential. After some time we recombine the wave-packets.
We start an interact sequence with $$ V/\hbar = \frac{1}{2} \begin{pmatrix} 0 & \Omega_R\\ \Omega_R & 0 \end{pmatrix} = \frac{1}{2} \begin{pmatrix} 0 & 2\pi f_R\\ 2\pi f_R & 0 \end{pmatrix}, $$ the Rabi-Hamiltonian in Dirac-picture with Rabi-frequency \(\Omega_R=2\pi f_R = 2\pi \cdot 2.5 \,\text{MHz}\). This means after \(400\, \mu \text{s}\) a full Rabi-cycle is achieved. Since we aim for a \(\frac{\pi}{2}\)-pulse, the sequence will be \(100\, \mu \text{s}\) long.
After achieving the equal superposition we subject both internal states to an harmonic potential, where one state is trapped by \( \omega_1 = 2\pi f_1 \) and the other by \( \omega_2 = 2\pi f_2 \): $$ V/\hbar = \begin{pmatrix} \frac{m}{2\hbar} \Big( 2\pi f_1 x \Big)^2 & 0\\ 0 & \frac{m}{2\hbar} \Big( 2\pi f_2 x \Big)^2 \end{pmatrix} $$ We chose the trapping frequencies to be \(f_1 = 100 \,\text{Hz} \) and \(f_2 = 2f_1 = 200 \,\text{Hz} \). After \(10\, \text{ms}\) of propagation time the first internal state will have made a complete evolution whilst the second will be finishing its second.
We reombine them with the same interact sequence that was used to generate the superposition. The XML-file that generates the above seen simulation reads:

<SIMULATION>
  <N_THREADS>4</N_THREADS>
  <DIM>1</DIM>
  <INTERNAL_DIM>2</INTERNAL_DIM>
  <FILENAME>0.000_1.bin</FILENAME>
  <FILENAME_2>0.000_2.bin</FILENAME_2>
  <ALGORITHM>
    <T_SCALE>1e-6</T_SCALE>
    <M>1.44466899e-25</M>
  </ALGORITHM>
  <CONSTANTS>
    <f_R>2500</f_R>
    <m>1.44466899e-25</m>
    <hbar>1.054571817e-34</hbar>
    <f_HO_1>1e2</f_HO_1>
    <f_HO_2>2e2</f_HO_2>
  </CONSTANTS>
  <SEQUENCE>
    <interact  dt="0.02" Nk="250" output_freq="packed" pn_freq="each"
      V_11_real="0" V_11_imag="0" V_12_real="2*pi*f_R/2" V_12_imag="0"
                                  V_22_real="0" V_22_imag="0"
    >100</interact>
  <freeprop dt="2" Nk="50" output_freq="packed" pn_freq="none"
    V_11_real="m/2/hbar*4*pi^2*f_HO_1^2*x^2" V_11_imag="0"  
    V_22_real="m/2/hbar*4*pi^2*f_HO_2^2*x^2" V_22_imag="0"
    >10000</freeprop>
    <interact dt="0.02" Nk="250" output_freq="packed" pn_freq="each"
      V_11_real="0" V_11_imag="0" V_12_real="2*pi*f_R/2" V_12_imag="0"
                                  V_22_real="0" V_22_imag="0"
    >100</interact>
  </SEQUENCE>
</SIMULATION>

Note:

The mass defined in the potential term has to be given a value in the <CONSTANTS> tag. The mass you provide the program in the <ALOGRITHM> tag is only for computing the kinetic part of the Schrödinger equation and will not be considered as a constant in the sequence items.