Momentum transfer in 2D harmonic trap

---

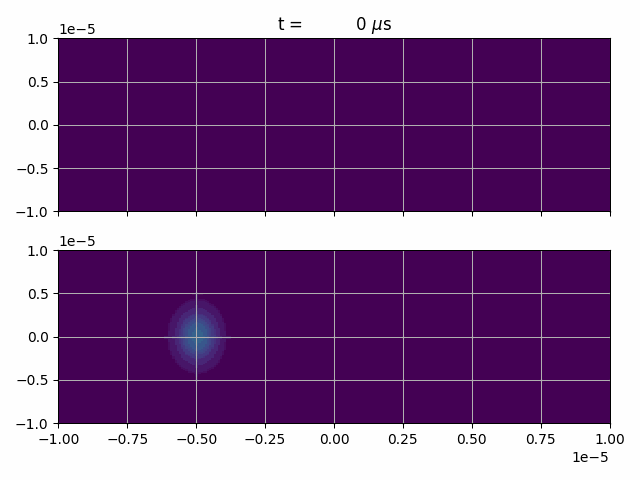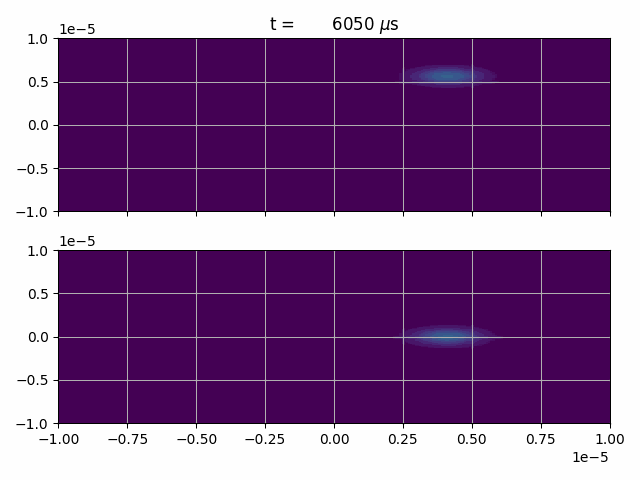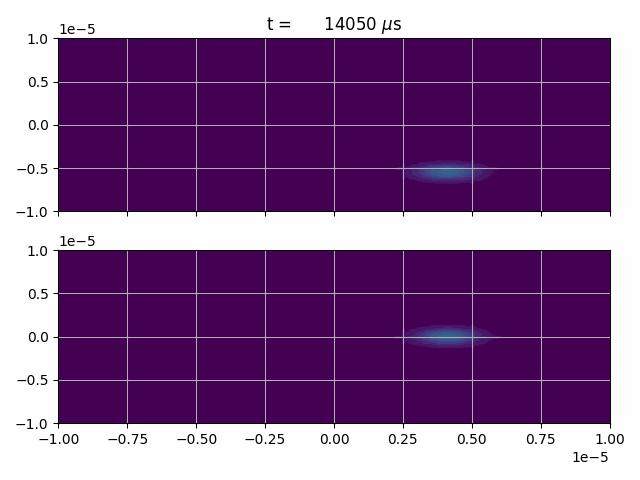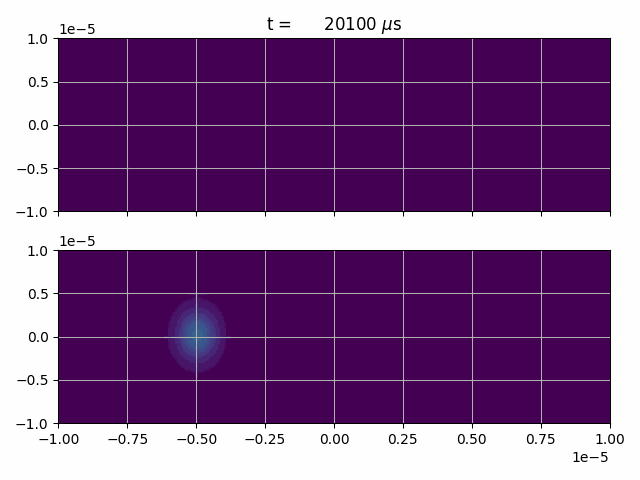
(You can find corresponding files in the TALISES examples folder)
In addition to the regular Rabi-Hamiltonian that only accounts for a time-dependent potential \(\propto e^{i\omega t}\) (which can be brought into a time-independent form by transforming into a rotating frame), we acknowledge in this example that the periodic potential that drives the transition is an electromagnetic wave and therefore has also a position-dependency such that the potential \(\propto e^{i\omega t+ i k x}\).
We start the time-propagation with an interact sequence with the potential $$ V(y,t)/\hbar = \frac{1}{2} \begin{pmatrix} 0 & 2\pi f_R \, e^{-iky}\\ 2\pi f_R\, e^{iky}& - \frac{\hbar k^2}{2m} \end{pmatrix}. $$ As mentioned above, the time-dependency was removed by going into the rotating frame. The periodic position-dependent potential leads to a change of the states momentun, since it is basically the position/momentum translation operator \(\hat{T}(k)|k'\rangle =e^{- i k x} |k'\rangle= |k'+k\rangle\).
The diagonal term is due to the fact that the excited state's energy additionaly differs by the kinetic energy \(\frac{\hbar^2k^2}{2m}\) if resonantly excited.
After creating an equal superposition, where the excited state recieves an additional momentum of \(\hbar k\) in y-direction, we switch on a 2D harmonic potential $$ V(x,y,t)/\hbar = \begin{pmatrix} \frac{m}{2\hbar} \Big(\big( 2\pi f_x x \big)^2 +\big( 2\pi f_y y \big)^2 \Big) & 0\\ 0 & \frac{m}{2\hbar} \Big(\big( 2\pi f_x x \big)^2 +\big( 2\pi f_y y \big)^2 \Big) \end{pmatrix}, $$ and let the wave-packets freely evolve for two evolutions, where we set \(f_x = 100\,\text{Hz} \) and \(f_y = 200\,\text{Hz} \). After this, we recombine both wave-packets with a sequence similar to the initial one, only that the light-field has an additional phase of \(\pi\), so that the probability amplitude completely transfers into the ground state again.
The XML-file reads

<SIMULATION>
  <N_THREADS>4</N_THREADS>
  <DIM>2</DIM>
  <INTERNAL_DIM>2</INTERNAL_DIM>
  <FILENAME>0.000_1.bin</FILENAME>
  <FILENAME_2>0.000_2.bin</FILENAME_2>
  <CONSTANTS>
    <m>1.44466899e-25</m>
    <hbar>1.054571817e-34</hbar>
    <f_R>5e3</f_R>
    <f_HO_x>100</f_HO_x>
    <f_HO_y>200</f_HO_y>
    <k>6e6</k>
  </CONSTANTS>
    <ALGORITHM>
      <M>1.44466899e-25</M>
      <T_SCALE>1e-6</T_SCALE>
   </ALGORITHM>
  <SEQUENCE>
    <interact Nk="25" dt="0.2" output_freq="packed" pn_freq="each"
        V_11_real="0" V_11_imag="0" 
        V_12_real="2*pi*f_R/2*cos(k*y)" V_12_imag="-2*pi*f_R/2*sin(k*y)"
        V_22_real="-hbar*k^2/2/m" V_22_imag="0"
    >50</interact>
    <freeprop Nk="100" dt="2" output_freq="packed" pn_freq="none"
        V_11_real="m/hbar/2*((2*pi*f_HO_x*x)^2+(2*pi*f_HO_y*y)^2)" V_11_imag="0" 
        V_22_real="m/hbar/2*((2*pi*f_HO_x*x)^2+(2*pi*f_HO_y*y)^2)" V_22_imag="0"
    >20000</freeprop> 
    <interact Nk="25" dt="0.2" output_freq="packed" pn_freq="each"
        V_11_real="0" V_11_imag="0"             
        V_12_real="2*pi*f_R/2*cos(k*y+pi)" V_12_imag="-2*pi*f_R/2*sin(k*y+pi)"
        V_22_real="-hbar*k^2/2/m" V_22_imag="0"
    >50</interact>
  </SEQUENCE>
</SIMULATION>