Bose-Einstein condensate collision

---

(You can find corresponding files in the TALISES examples folder)
The time-evolution of Bose-Einstein condensates (BECs) is under certain approximations well described by a nonlinear Schrödinger equation called the Gross-Pitaevskii equation $$ i\frac{\partial}{\partial t} \Psi = -\frac{\hbar}{2m}\nabla^2 \Psi + \frac{1}{\hbar}V \Psi + \frac{1}{\hbar} g |\Psi |^2 \Psi.
$$ It is an effective single particle, nonlinear Schrödinger equation describing the collective behaviour of degenerate Bosons. The nonlinear term is accounting for interparticle scattering processes with strength \(g = \frac{4\pi \hbar^2 a}{m}\), where \(a\) is the s-scatter length.
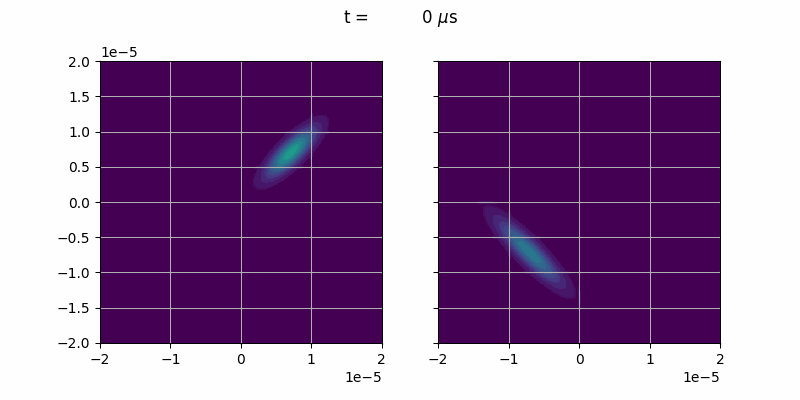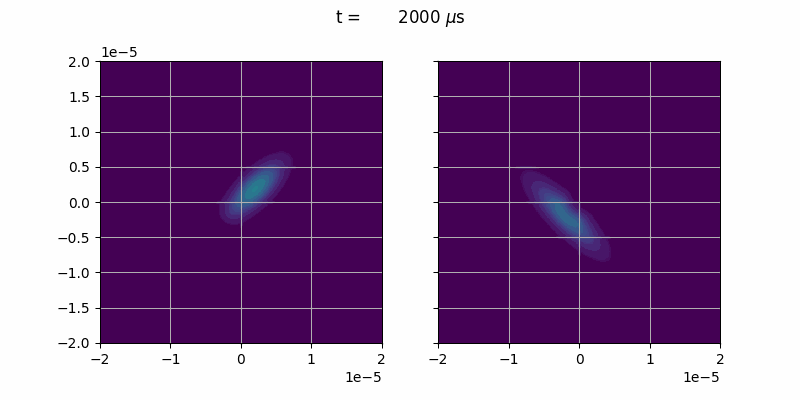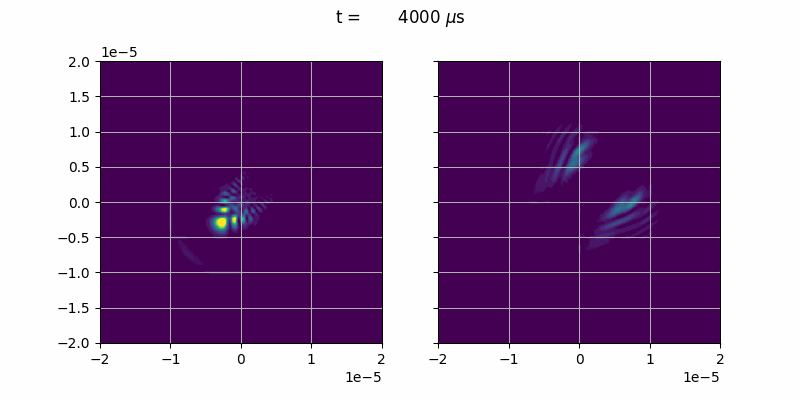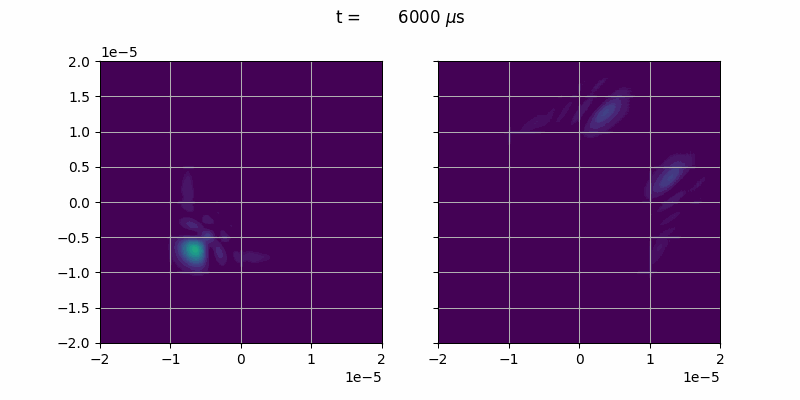
This scatter length can be different for different particles and even internal states. We will simulate the collision of two BECs in different, orthogonal states. This could mean that the BECs are made of the same atoms but in different internal states, or even entirely different atomic species.
Since we will otherwise assume that \(V=0\), the Hamiltonian is $$ H = -\frac{\hbar^2}{2m}\nabla^2 + \begin{pmatrix} g_{11} |\Psi_1 |^2 + g_{12} |\Psi_2 |^2 & 0\\ 0 & g_{21} |\Psi_1 |^2 + g_{22} |\Psi_2 |^2 \end{pmatrix}. $$

In order make two BECs collide we give them an initial momentum in opposite direction. Furthermore we rotate the coordinate system a bit, so it looks cooler.
The first BEC is defined by

<SIMULATION>
  <DIM>2</DIM> 
  <FILENAME>0.000_1.bin</FILENAME>
  <PSI_REAL_2D>exp( -0.25*((cos(phi)*x+sin(phi)*y-x_0)/sigma_x)^2 )*exp( -0.25*((-sin(phi)*y+cos(phi)*x-y_0)/sigma_y)^2 )*cos(k*(cos(phi)*x+sin(phi)*y))</PSI_REAL_2D>
  <PSI_IMAG_2D>exp( -0.25*((cos(phi)*x+sin(phi)*y-x_0)/sigma_x)^2 )*exp( -0.25*((-sin(phi)*y+cos(phi)*x-y_0)/sigma_y)^2 )*sin(k*(cos(phi)*x+sin(phi)*y))</PSI_IMAG_2D>
  <CONSTANTS>
    <N>1e5</N>
    <phi>0.78</phi>
    <k>5e6</k>
    <x_0>-10e-6</x_0>
    <y_0>0</y_0>
    <sigma_x>1e-6</sigma_x>
    <sigma_y>4e-6</sigma_y>
  </CONSTANTS>
   <ALGORITHM>
    <NX>512</NX>
    <NY>512</NY>
    <XMIN>-20e-6</XMIN><XMAX>20e-6</XMAX>
    <YMIN>-20e-6</YMIN><YMAX>20e-6</YMAX>
    </ALGORITHM>
</SIMULATION>

We offset it by \(-10\mu\text{m}\) in the x-direction and then rotate it by \(\phi = \pi / 4\). Note that it is normalized to \(\int \text{d}r |\Psi |^2 = N = 10^{5}\). We thus assume the BEC comprises of \(10^{5}\) atoms.
The second BEC is generated with

<SIMULATION>
  <DIM>2</DIM> 
  <FILENAME>0.000_2.bin</FILENAME>
  <PSI_REAL_2D>exp( -0.25*((cos(phi)*x+sin(phi)*y-x_0)/sigma_x)^2 )*exp( -0.25*((-sin(phi)*y+cos(phi)*x-y_0)/sigma_y)^2 )*cos(k*(cos(phi)*x+sin(phi)*y))</PSI_REAL_2D>
  <PSI_IMAG_2D>exp( -0.25*((cos(phi)*x+sin(phi)*y-x_0)/sigma_x)^2 )*exp( -0.25*((-sin(phi)*y+cos(phi)*x-y_0)/sigma_y)^2 )*sin(k*(cos(phi)*x+sin(phi)*y))</PSI_IMAG_2D>
  <CONSTANTS>
    <N>1e5</N>
    <phi>-2.35</phi>
    <k>5e6</k>
    <x_0>-10e-6</x_0>
    <y_0>0</y_0>
    <sigma_x>3e-6</sigma_x>
    <sigma_y>1e-6</sigma_y>
  </CONSTANTS>
   <ALGORITHM>
    <NX>512</NX>
    <NY>512</NY>
    <XMIN>-20e-6</XMIN><XMAX>20e-6</XMAX>
    <YMIN>-20e-6</YMIN><YMAX>20e-6</YMAX>
    </ALGORITHM>
</SIMULATION>

This one is also offset by \(-10\mu\text{m}\) in the x-direction but then rotated by \(\phi = -\frac{3\pi}{4}\).
The time-propagation xml reads

<SIMULATION>
  <N_THREADS>4</N_THREADS>
  <DIM>2</DIM>
  <INTERNAL_DIM>2</INTERNAL_DIM>
  <FILENAME>0.000_1.bin</FILENAME>
  <FILENAME_2>0.000_2.bin</FILENAME_2>
  <CONSTANTS>
  <g_11>1e-14</g_11>
  <g_12>5e-12</g_12>
  <g_21>5e-12</g_21>
  <g_22>1e-14</g_22>
  </CONSTANTS>
    <ALGORITHM>
      <M>1.44466899e-25</M>
      <T_SCALE>1e-6</T_SCALE>
   </ALGORITHM>
  <SEQUENCE>
    <freeprop Nk="50" dt="2" output_freq="packed" pn_freq="none"
    V_11_real="g_11*(psi_1_real^2+psi_1_imag^2)+g_12*(psi_2_real^2+psi_2_imag^2)" V_11_imag="0" 
    V_22_real="g_21*(psi_1_real^2+psi_1_imag^2)+g_22*(psi_2_real^2+psi_2_imag^2)" V_22_imag="0"
    >6000</freeprop> 
  </SEQUENCE>
</SIMULATION>

Note that \(|\Psi|^2 = (\text{Re}\Psi)^2 + (\text{Im}\Psi)^2\). We give the BEC an especially strong scattering strength accros internal states \(g_{12}=g_{21} >> g_{11} = g_{22}\).