Stimulated Raman transitions

---

(You can find corresponding files in the TALISES examples folder)
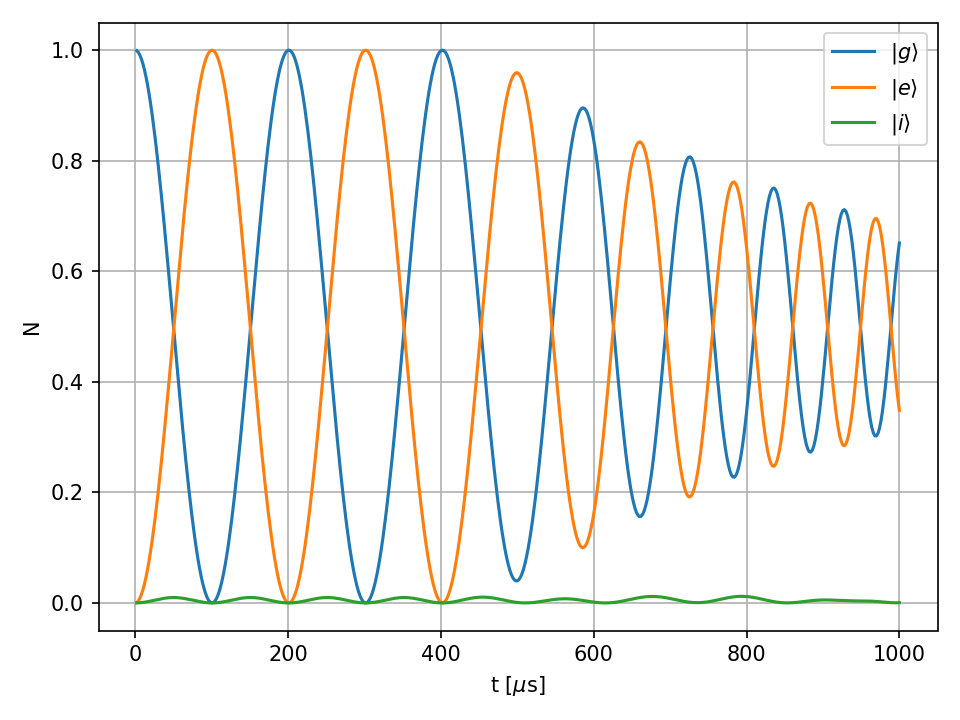
In this example we simulate a three-level system undergoing stimulated two-photon transition across an intermediate state that will only be sparsely populated during the process. The three levels comprise of a ground, excited and intermediate state \( |g\rangle,|e\rangle,|i\rangle \).
Furthermore, we have two laser as time-periodic potentials \(\omega_\mathrm{S}, \omega_\mathrm{P}\). A coupling exists only between \( |g\rangle \leftrightarrow |i\rangle \leftrightarrow |e\rangle \), but not \(|g\rangle \nleftrightarrow |e\rangle\).
The potential part of the Hamiltonian is $$ V(t)/\hbar = \displaystyle \left[\begin{matrix} \omega_{g} & 0 & \frac{\Omega_{gi} e^{i \omega_{P} t}}{2}\\ 0 & \omega_{e} & \frac{\Omega_{ei} e^{i \omega_{S} t}}{2}\\ \frac{\Omega_{gi} e^{- i \omega_{P} t}}{2} & \frac{\Omega_{ei} e^{- i \omega_{S} t}}{2} & \omega_{i}\end{matrix}\right] $$ A sketch of this level system looks like this

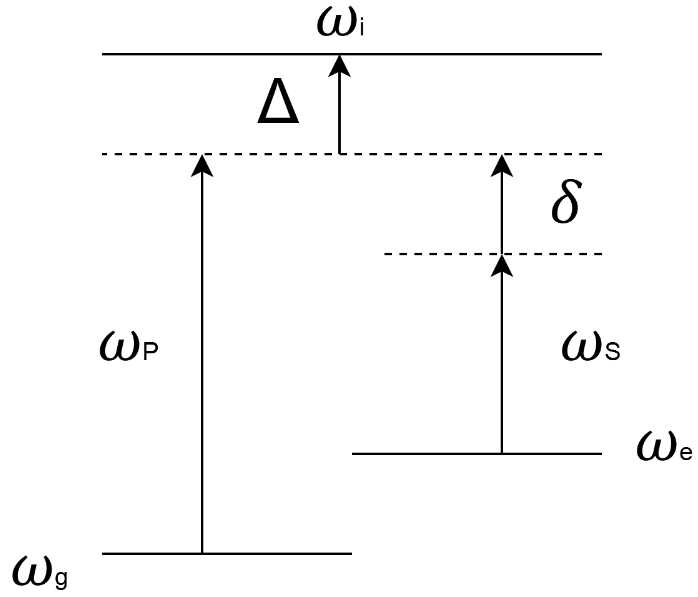
where we additionally defined \(\omega_i-\omega_\mathrm{P}-\omega_g=\Delta\) and \(\omega_\mathrm{P}-\omega_\mathrm{S}-\omega_e+\omega_g = \delta\). Usually \(\Delta\) is called the one-photon detuning, and \(\delta\) the two-photon detuning. One can transform the above stated potential to a time-independent form $$ V(t)/\hbar = \displaystyle \left[\begin{matrix} 0 & 0 & \frac{\Omega_{gi} }{2}\\ 0 & \delta & \frac{\Omega_{ei} }{2}\\ \frac{\Omega_{gi} }{2} & \frac{\Omega_{ei} }{2} & \Delta\end{matrix}\right] $$ which is much better to simulate in terms of computational demand.
For our simulation we take \(\Omega_{gi} = \Omega_{ei} = 100\, \text{kHz}/2\pi\) and \(\Delta=1 \,\text{MHz}/2\pi \). From analytical results one can calculate that the generalized Rabi frequency between excited and ground state is \( \tilde{\Omega}_R = \frac{1}{4\Delta}\Omega_{gi}\Omega_{ei} = 10\,\text{kHz}/ 2\pi\).
Thus, one Rabi-cycle takes \(200\, \mu \text{s}\). We drive two Rabi-cycles resonantly, and after \(400\, \mu \text{s}\) slowly start to increase the two-photon detuning from \(\delta = 0\) by a rate of \(0.1 \,\text{kHz}/\mu\text{s}\).
The XML-file reads

<SIMULATION>
  <N_THREADS>4</N_THREADS>
  <DIM>1</DIM>
  <INTERNAL_DIM>3</INTERNAL_DIM>
  <FILENAME>0.000_1.bin</FILENAME>
  <FILENAME_2>0.000_2.bin</FILENAME_2>
  <FILENAME_3>0.000_2.bin</FILENAME_3>
  <ALGORITHM>
    <T_SCALE>1e-6</T_SCALE>
    <M>1.44466899e-25</M>
  </ALGORITHM>
  <CONSTANTS>
    <f_gi>1e5</f_gi>
    <f_ei>1e5</f_ei>
    <f_Delta>1e6</f_Delta>
    <f_delta>2e3</f_delta>
    <t0>400e-6</t0>
    <Dt>100e-6</Dt>
  </CONSTANTS>
  <SEQUENCE>
    <interact Nk="1" dt="2" output_freq="packed" pn_freq="each"
        V_11_real="0" V_11_imag="0"  
        V_12_real="0" V_12_imag="0"   
        V_13_real="2*pi*f_gi/2" V_13_imag="0"
        V_22_real="2*pi*f_delta*(1/2+1/2*sign(t-t0))*((t-t0)/Dt)" V_22_imag="0"   
        V_23_real="2*pi*f_ei/2" V_23_imag="0"
        V_33_real="2*pi*f_Delta" V_33_imag="0"
    >1000</interact>
  </SEQUENCE>
</SIMULATION>