Potential Barrier

---

(You can find corresponding files in the TALISES examples folder)
Even though one of TALISES' specialties lies in the simple incoorperation of mutiple internal degrees of freedom, you can also just time-propagate wave-functions with no internal structure.
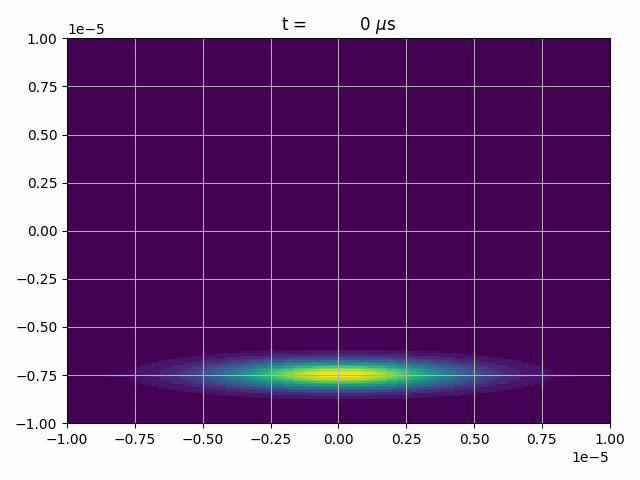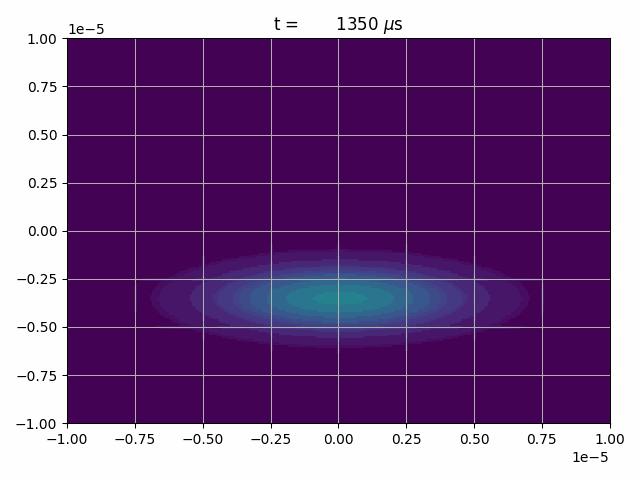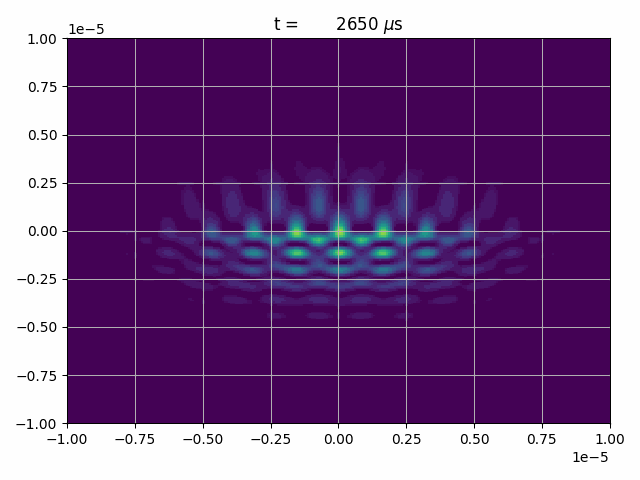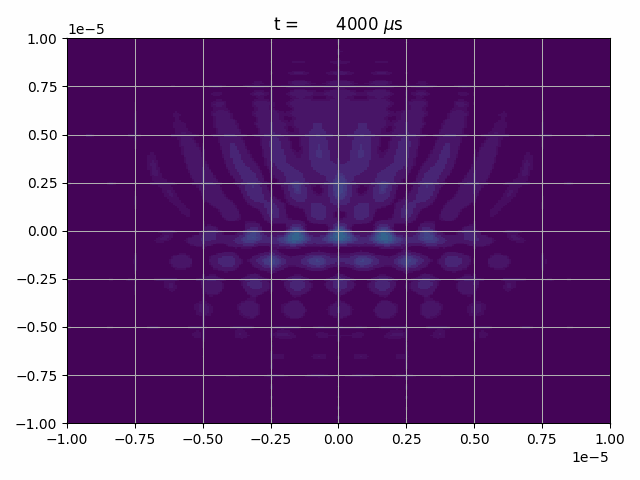
As an example we will let a Gaussian wave-packet hit a potential-barrier that will be a box-potential in y-direction and a periodic box-potential in x-direction.

Box potentials

From the build-in functions that come with the muparser libary we will use the sign function $$ \text{sign}(x):={\begin{cases}-1&{\text{if }}x<0,\\0&{\text{if }}x=0,\\1&{\text{if }}x>0.\end{cases}} $$ to generate a box-potential. The sign function can be used to construct the Heaviside step function $$ \theta (x) = \frac{1}{2}\Big(1+\text{sign}(x)\Big). $$ and a box-function, which in terms of a Heaviside step function or sign function is $$ \text{rect} (x) = \theta\Big(x-\frac{1}{2}\Big) \cdot \theta\Big(\frac{1}{2}-x\Big) = \theta\Big(x+\frac{1}{2}\Big) - \theta\Big(x-\frac{1}{2}\Big) \\ \text{and} \\ \text{rect} (x) = \frac{1}{2}\Big[ \text{sign}\Big(x+\frac{1}{2}\Big) - \text{sign}\Big(x-\frac{1}{2}\Big) \Big]. $$ A periodic box function can be generated using the \(\text{rint}(x)\) function, which rounds a number to the nearest integer. If we supply it with a simple harmonic function as in \( \text{rint}((\sin k_B x)^2) \) (where \(k_B\) is a measure of periodicity), we will have a nice perdiodic box function.
Our potential is then $$ V(x,y) = A \bigg[ \frac{1}{4} \bigg( 1+ \text{sign}(y-y_l) \bigg)\cdot \bigg( 1+ \text{sign}(y_u-y) \bigg)\cdot \text{rint}((\sin k_B x)^2) \bigg], $$ where \(y_l\) and \(y_u\) are the lower and upper bound of the potential-box.
The XML file giving the above time-propagation reads

<SIMULATION>
  <N_THREADS>4</N_THREADS>
  <DIM>2</DIM>
  <INTERNAL_DIM>1</INTERNAL_DIM>
  <FILENAME>0.000_1.bin</FILENAME>
  <CONSTANTS>
    <barrier_upper_ybound>.1e-6</barrier_upper_ybound>
    <barrier_lower_ybound>-.1e-6</barrier_lower_ybound>
    <barrier_Amp>1e5</barrier_Amp>
    <kx_barrier>2e6</kx_barrier>
  </CONSTANTS>
  <ALGORITHM>
    <M>1.44466899e-25</M>
    <T_SCALE>1e-6</T_SCALE>
  </ALGORITHM>
  <SEQUENCE>
    <freeprop Nk="25" dt="2" output_freq="packed" pn_freq="none"
    V_11_real="(1/2*(1+sign(y-barrier_lower_ybound))*1/2*(1+sign(-y+barrier_upper_ybound)) 
    * rint(sin(kx_barrier*x)^2))*barrier_Amp" 
    V_11_imag="0"
    >4000</freeprop> 
  </SEQUENCE>
</SIMULATION>