Generating a wave-function

The gen_psi_0 utility program

TALISES comes with two executable programs, one of which is gen_psi_0. While the main program does the heavy-duty calculations for wave-function's time-propagation, gen_psi_0 is generating the initial wave-function.
The gen_psi_0 program requires an XML file as input in order to generate a binary data file containing the wave-functions information.
In the next few sections we generate some exemplary wave-functions.

Generating a 1D wave-function

The XML file needs to include the following tags

These tags are encapsulated in the <SIMULATION> parrent. A wave function of Gaussian appearance can be generated with

<SIMULATION>
  <DIM>1</DIM>
  <FILENAME>0.000_1.bin</FILENAME>
  <PSI_REAL_1D>exp( -0.25*((x-x_0)/sigma_x)^2 )</PSI_REAL_1D>
  <PSI_IMAG_1D>0</PSI_IMAG_1D>
  <ALGORITHM>
    <NX>256</NX>
    <XMIN>-10e-6</XMIN>
    <XMAX>10e-6</XMAX>
  </ALGORITHM>
  <CONSTANTS>
    <N>1</N>
    <x_0>0</x_0>
    <sigma_x>1e-6</sigma_x>
  </CONSTANTS>
</SIMULATION>

Within the <CONSTANTS> tag one can define numeric values for constants used in the <PSI_****_1D> tag.
Since C++ does not support complex numbers natively, we define real and imaginary part seperately. For example, if you would like to give the wave-function an initial momentum \(\hbar k\) $$ \Psi \approx \exp \Big[-\Big(\frac{x-x_0}{2\sigma_x}\Big)^2 + i k x \Big] $$ the tags would read

<PSI_REAL_1D>exp( -0.25*((x-x_0)/sigma_x)^2 ) * cos(k*x)</PSI_REAL_1D>
<PSI_IMAG_1D>exp( -0.25*((x-x_0)/sigma_x)^2 ) * sin(k*x)</PSI_IMAG_1D>

<N> is a normalization constant. The program normalizes the wave-functions, such that \( \int \mathrm{d}\vec{r} |\Psi|^2 = N\).
Within <ALGORITHM> we define important numbers necessary for the discretization of the spatial grid such as <NX>, <XMIN> and <XMAX>.

If we save this file as gauss.xml we can generate the wave-function with

gen_psi_0 gauss.xml

This creates a file named 0.000_1.bin in the current working directory.
TALISES generated data can be easily handled with the python package talisestools. You can install it via the python package manager using

pip install talisestools

(More details on the package's funcionallity is described in Handling binary data)
We can have a look at the wave-function by using talisestools' plotbin function in python 

import talisestools as tt
tt.plotbin("0.000_1.bin")

This will create a .png file which should look like this

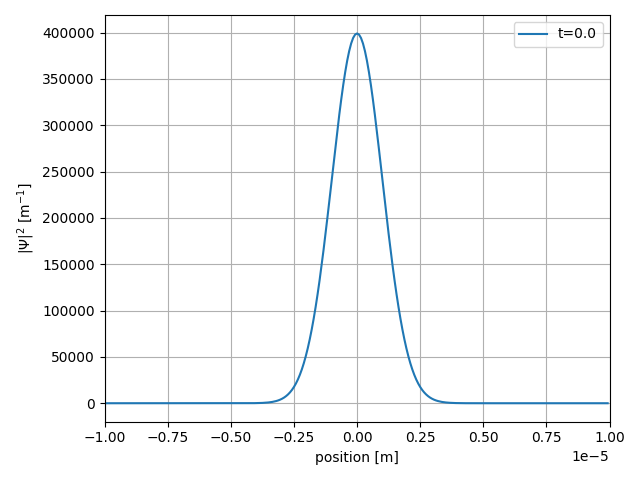
1D Gaussian wave-function plot

Naturally, TALISES uses SI units for all computations.

Generating a 2D wave-function

Following the previous example it is very straightfoward to extend the XML file to generate a wave-function in two dimensions. This time we create a 2D Gaussian wave-function centered at \(x_0=-5\mu\text{m}\), \(y_0=0\) and width \(\sigma_x=0.5\mu\text{m}\), \(\sigma_y = 2\mu\text{m}\). 

<SIMULATION>
  <DIM>2</DIM> 
  <FILENAME>0.000_1.bin</FILENAME>
  <PSI_REAL_2D>exp( -0.25*((x-x_0)/sigma_x)^2 )*exp( -0.25*((y-y_0)/sigma_y)^2 )</PSI_REAL_2D>
  <PSI_IMAG_2D>0</PSI_IMAG_2D>
  <CONSTANTS>
    <N>1</N>
    <x_0>-5e-6</x_0>
    <y_0>0</y_0>
    <sigma_x>0.5e-6</sigma_x>
    <sigma_y>2e-6</sigma_y>
  </CONSTANTS>
   <ALGORITHM>
    <NX>256</NX>
    <NY>256</NY>
    <XMIN>-10e-6</XMIN><XMAX>10e-6</XMAX>
    <YMIN>-10e-6</YMIN><YMAX>10e-6</YMAX>
    </ALGORITHM>
</SIMULATION>

If you plot the resulting binary file using the plotbin function you will see something like this

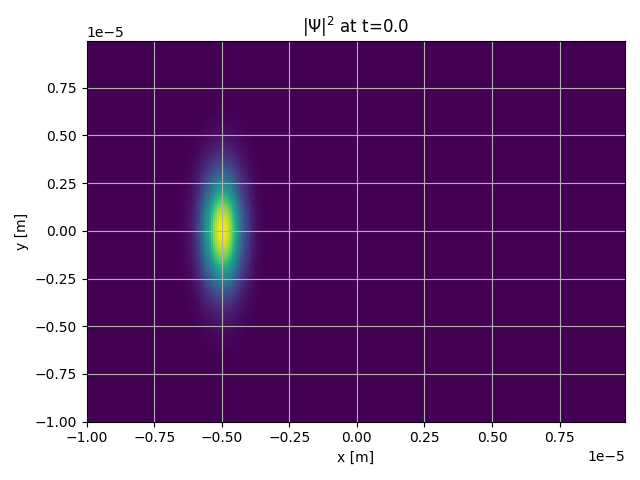
1D Gaussian wave-function plot

You can be much more creative with you wave-functions, for example

1/2*(sign(x--8)+sign(-x+3))*abs(sin(1/8*(x^2+y^2))*sin(2*(x+y)))*exp(-0.25*(y/3)^2)

will give you

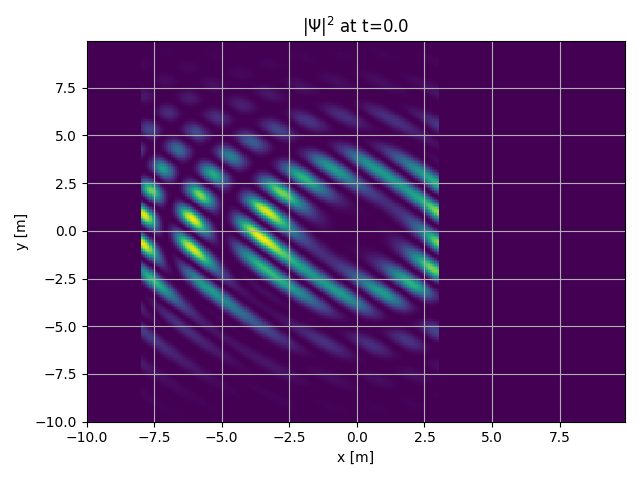
1D Gaussian wave-function plot

Built-in functions

The muparser libary allows for following functions

Name Argc. Explanation
sin 1 sine function
cos 1 cosine function
tan 1 tangens function
asin 1 arcus sine function
acos 1 arcus cosine function
atan 1 arcus tangens function
sinh 1 hyperbolic sine function
cosh 1 hyperbolic cosine
tanh 1 hyperbolic tangens function
asinh 1 hyperbolic arcus sine function
acosh 1 hyperbolic arcus tangens function
atanh 1 hyperbolic arcur tangens function
log2 1 logarithm to the base 2
log10 1 logarithm to the base 10
log 1 logarithm to base e (2.71828...)
ln 1 logarithm to base e (2.71828...)
exp 1 e raised to the power of x
sqrt 1 square root of a value
sign 1 sign function -1 if x<0; 1 if x>0
rint 1 round to nearest integer
abs 1 absolute value
min var. min of all arguments
max var. max of all arguments
sum var. sum of all arguments
avg var. mean value of all arguments

Importance of sampling frequency

The split-step Fourier method uses position and momentum space to calculate the wave-function's time-propagation. Therefore, one hast to keep in mind that the momentum state of the wave-function can only be correctly accounted for if the space-grid has enough sampling points.
This means that if \(\Delta x\) is the whole position space consisting of \(N\) samples, we have a sampling rate of \(\delta x = \Delta x / N\). If we Fourier transform any wave-form, we can safely represent momentum states within \(\Delta k = 2\pi / \delta x\). The sampling rate in momentum space is \(\delta k = 2\pi / \Delta x\).