Propagate the wave-function
(You can find corresponding files in the TALISES examples folder)
The heart of TALISES lies in the ability to propagate a wave-function
\( \hat{U} |\Psi(r,t_0)\rangle = |\Psi(r,t)\rangle\) in accordance to the Schrödinger equation
The configuration of the time-propagation and Hamiltonian is done using an XML-configuration file. Important XML-tags are:
<N_THREADS>: number of threads used by program<DIM>: number of spatial dimensions<INTERNAL_DIM>: number of internal degrees of freedom<FILENAME>: name of the binary file representing the wave-function generated by gen_psi_0. There need to be as many files as internal degrees of freedom<M>: mass \(m\) used in the kinetic term of the Schrödinger equation.<T_SCALE>: convenient scaling factor for time units in sequence attributes<CONSTANTS>: here we define constants used in the Hamiltonian's expression<SEQUENCE>: here we declare the Hamiltonian and which numerical procedure to use
Sequence items <interact> and <freeprop>
There are two types of sequences: <interact> and <freeprop>. Before we explain the differences, let us see what they have in common. A sequence might look like this
<SEQUENCE>
<freeprop dt="2" Nk="20" output_freq="packed" pn_freq="each"
V_11_real="0" V_11_imag="0"
V_22_real="0" V_22_imag="0"
>1000</freeprop>
<interact dt="0.02" Nk="500" output_freq="packed" pn_freq="each"
V_11_real="0" V_11_imag="0" V_12_real="0" V_12_imag="0"
V_22_real="0" V_22_imag="0"
>1000</interact>
</SEQUENCE>
A sequence item tells the programm what the matrix elements of the potential term \(\hat{V}/\hbar\) are.
For this one must define the attributes V_ij_real and V_ij_imag in the sequence item.
Just as in the generation of the initial wavefunction, the real and imaginary part are stated seperately.
Predefined constants and variables your can use are pi and e and x, y, z, t and the real and imaginary
probabillity amplitudes psi_j_real and psi_j_imag (\(j\) denotes the corresponding internal state).
Furthermore, you can use the build-in functions from the muparser libary in the matrix elements.
Attributes:
dt: time-step increment
Nk: number of time steps after which the wave-function is saved
output_freq: defines how the wave-function is saved.
"each" saves the wavefunction after every \(N_k\)-th step as a seperate file
"packed" saves the wavefunction after every \(N_k\)-th step and appends it to an existing file
"last" saves the wavefunction just at the last time-step
pn_freq: can be used in order the evluate the particle number in the internal states.
"each" evaluated population after every \(N_k\)-th step
"last" evaluated population just at the last time-step
"none" does nothing
The length of time the sequence is supposed to be executed is the value of the sequence item. In the above example both sequences, <interact> and <freeprop>, are lasting 1000 seconds. The time units can be scaled via the <T_SCALE> tag. For example, if we set <T_SCALE>1e-6</T_SCALE> the time units in the sequence attributes become \(\mu\)s, which can be easier to read.
Now to the simple difference between <interact> and <freeprop>:
interact invokes a numerical diagonalization of the internal state Hamiltonian \(V\).
This has to be used when the potential term is not diagonal and interactions between the states are simulated.
freeprop can be used when the potential is diagonal and is hence faster in computinng the time-propagation.
You do not need to define off-diagonal matrix elements in a freeprop sequence item.
Example
(You can find this example in the TALISES examples folder)
First let us generate a simple 1D Gaussian wavepacket
%gauss.xml
<SIMULATION>
<DIM>1</DIM>
<FILENAME>0.000_1.bin</FILENAME>
<PSI_REAL_1D>exp( -0.25*((x-x_0)/sigma_x)^2 )</PSI_REAL_1D>
<PSI_IMAG_1D>0</PSI_IMAG_1D>
<ALGORITHM>
<NX>256</NX>
<XMIN>-10e-6</XMIN>
<XMAX>10e-6</XMAX>
</ALGORITHM>
<CONSTANTS>
<N>1</N>
<x_0>0</x_0>
<sigma_x>1e-6</sigma_x>
</CONSTANTS>
</SIMULATION>
and a second, empty internal state which shall be the excited state
%zero.xml
<SIMULATION>
<DIM>1</DIM>
<FILENAME>0.000_2.bin</FILENAME>
<PSI_REAL_1D>0</PSI_REAL_1D>
<PSI_IMAG_1D>0</PSI_IMAG_1D>
<ALGORITHM>
<NX>256</NX>
<XMIN>-10e-6</XMIN>
<XMAX>10e-6</XMAX>
</ALGORITHM>
<CONSTANTS>
<N>1</N>
</CONSTANTS>
</SIMULATION>
Generate the wave-functions by typing
gen_psi_0 gauss.xml
gen_psi_0 zero.xml
The time-propagation is defined by the following code
%timeprop.xml
<SIMULATION>
<N_THREADS>4</N_THREADS>
<DIM>1</DIM>
<INTERNAL_DIM>2</INTERNAL_DIM>
<FILENAME>0.000_1.bin</FILENAME>
<FILENAME_2>0.000_2.bin</FILENAME_2>
<ALGORITHM>
<T_SCALE>1e-6</T_SCALE>
<M>5e-26</M>
</ALGORITHM>
<CONSTANTS>
<f_R>2500</f_R>
</CONSTANTS>
<SEQUENCE>
<freeprop dt="2" Nk="20" output_freq="packed" pn_freq="each"
V_11_real="0" V_11_imag="0"
V_22_real="0" V_22_imag="0"
>1000</freeprop>
<interact dt="0.02" Nk="500" output_freq="packed" pn_freq="each"
V_11_real="0" V_11_imag="0" V_12_real="2*pi*f_R/2" V_12_imag="0"
V_22_real="0" V_22_imag="0"
>1000</interact>
<freeprop dt="2" Nk="20" output_freq="packed" pn_freq="each"
V_11_real="0" V_11_imag="0"
V_22_real="0" V_22_imag="0"
>1000</freeprop>
</SEQUENCE>
</SIMULATION>
and execute the time-propagation with
talises timeprop.xml
Step-by-step examination
We go through timeprop.xml line by line:
<N_THREADS>4</N_THREADS>
<DIM>1</DIM>
<INTERNAL_DIM>2</INTERNAL_DIM>
We declare to use 4 threads for our simulation of a spatially one dimensional wave-function with two internal degrees of freedom
<FILENAME>0.000_1.bin</FILENAME>
<FILENAME_2>0.000_2.bin</FILENAME_2>
We specify the file paths of the wave-functions generated by gen_psi_0.
We load the files as the two internal states of which one is the Gaussian wave-packet and the other one empty.
Note: the file paths are relative to your working directory.
<ALGORITHM>
<T_SCALE>1e-6</T_SCALE>
<M>5e-26</M>
</ALGORITHM>
We scale the time attributes in our sequence items, so that they are given in \(\mu\)s.
The mass of the particle is \(m=5\cdot 10^{-25} \,\text{kg}\).
Note: The parameter <M> defines the mass in the kinetic term of the Schrödinger equation nad thus only affects the kinetic term.
<CONSTANTS>
<f_R>2500</f_R>
</CONSTANTS>
We define one constant \(f_R\) which we can use later on in the description of the potential matrix-elements \(V\)
<SEQUENCE>
<freeprop dt="2" Nk="20" output_freq="packed" pn_freq="each"
V_11_real="0" V_11_imag="0"
V_22_real="0" V_22_imag="0"
>1000</freeprop>
The sequence starts with a \(1000\, \mu \text{s}\) long freeprop item. The time-steps are \(2\, \mu \text{s}\) long and the wave-function will be saved every 20th step. The wave-packet freely propagates.
<interact dt="0.02" Nk="500" output_freq="packed" pn_freq="each"
V_11_real="0" V_11_imag="0" V_12_real="2*pi*f_R/2" V_12_imag="0"
V_22_real="0" V_22_imag="0"
>1000</interact>
We start a \(1000\, \mu \text{s}\) interact sequence with
$$
V/\hbar = \frac{1}{2}
\begin{pmatrix}
0 & \Omega_R\\
\Omega_R & 0
\end{pmatrix}
=
\frac{1}{2}
\begin{pmatrix}
0 & 2\pi f_R\\
2\pi f_R & 0
\end{pmatrix}.
$$
The Rabi-Hamiltonian in Dirac-picture and Rabi-frequency \(\Omega_R=2\pi f_R = 2\pi \cdot 2.5 \,\text{MHz}\), as defined in the <CONSTANTS> item.
<freeprop dt="2" Nk="20" output_freq="packed" pn_freq="each"
V_11_real="0" V_11_imag="0"
V_22_real="0" V_22_imag="0"
>1000</freeprop>
</SEQUENCE>
</SIMULATION>
After some Rabi-cycles we let the wave-packets freely expand again.
Plotting the result
Start python, load talisestools und use the readall function to extract the data from the binaries.
import talisestools as tt
## Load binary data
data_psi1 = tt.readall(1)
data_psi2 = tt.readall(2)
# Get information for plots
psi1 = data_psi1["wavefunction"]
psi2 = data_psi2["wavefunction"]
t = data_psi1["t"]
xMin = data_psi1["xMin"]
xMax = data_psi1["xMax"]
nDimX = data_psi1["nDimX"]
With this we can start to create a animation of the wave-functions time-evolution.
import numpy as np
from matplotlib import pyplot as plt
x = np.linspace(xMin, xMax, nDimX)
max_density = np.max(np.abs(psi1)**2)
## Create animated gif
import gif
@gif.frame
def plot(psi1, psi2, x, t, max_density):
den1_real = np.abs(np.real(psi1))**2
den2_real = np.abs(np.real(psi2))**2
den1_imag = np.abs(np.imag(psi1))**2
den2_imag = np.abs(np.imag(psi2))**2
den1 = den1_real + den1_imag
den2 = den2_real + den2_imag
fig, (ax1, ax2) = plt.subplots(2, sharex=True)
ax1.set_title(r"t = {:10.0f} $\mu$s".format(t))
ax1.plot(x, den2, label = r"$|\Psi|^2$")
ax1.plot(x, den2_real, label = r"|real$(\Psi|)^2$")
ax1.plot(x, den2_imag, label = r"|imag$(\Psi|)^2$")
ax1.set_ylabel(r"$|\Psi|^2$ [m$^{-1}$] excited")
ax2.plot(x, den1, label = r"$|\Psi|^2$")
ax2.plot(x, den1_real, label = r"|real$(\Psi|)^2$")
ax2.plot(x, den1_imag, label = r"|imag$(\Psi|)^2$")
ax2.set_ylabel(r"$|\Psi|^2$ [m$^{-1}$] ground")
ax2.set_xlabel(r"position [m]")
ax1.set_xlim(np.min(x), np.max(x))
ax1.set_ylim(0, max_density)
ax2.set_ylim(0, max_density)
ax1.legend()
ax2.legend()
ax1.grid()
ax2.grid()
plt.tight_layout()
frames = []
for i in range(0,len(t)):
frame = plot(psi1[:,i], psi2[:,i], x, t[i], max_density)
frames.append(frame)
print("Generated plot "+str(i)+"/"+str(len(t)-1))
gif.save(frames, "eval.gif", duration=100)
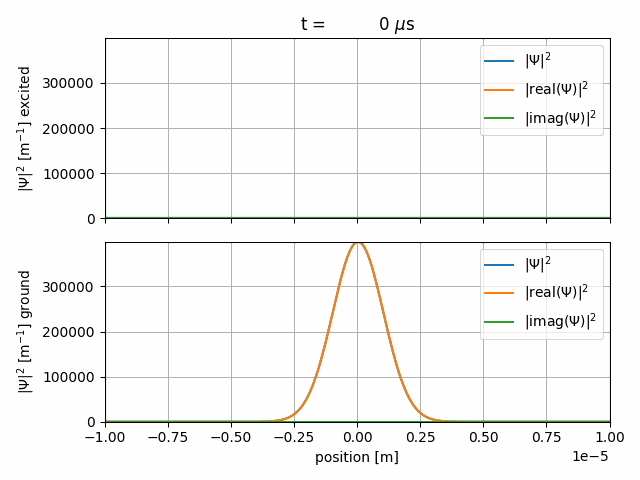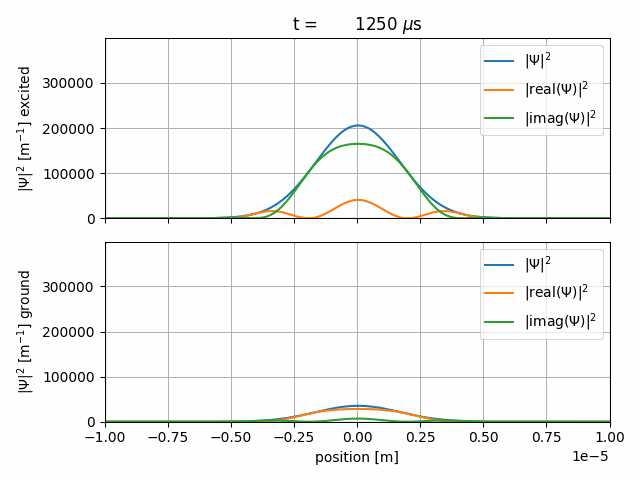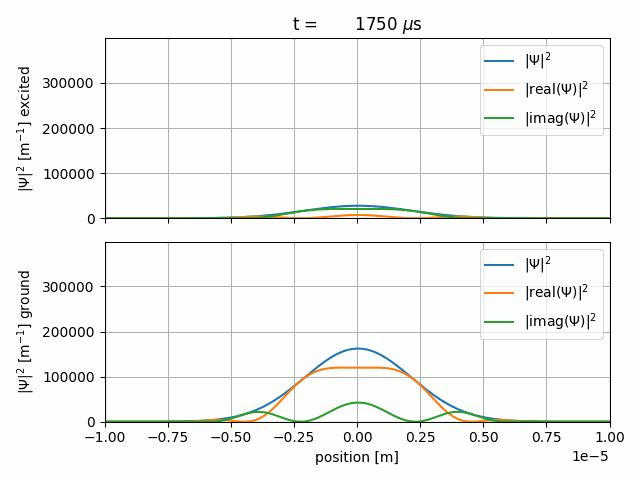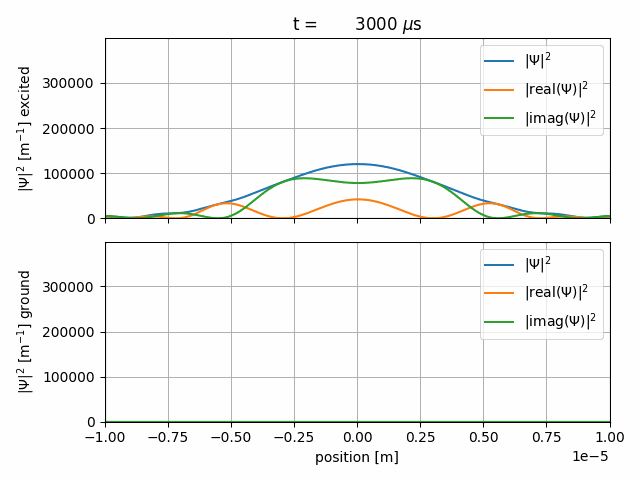
The resulting gif should look like this
